GIAN course on
Graphs, Spectra and Convex Geometry
Completed
Overview
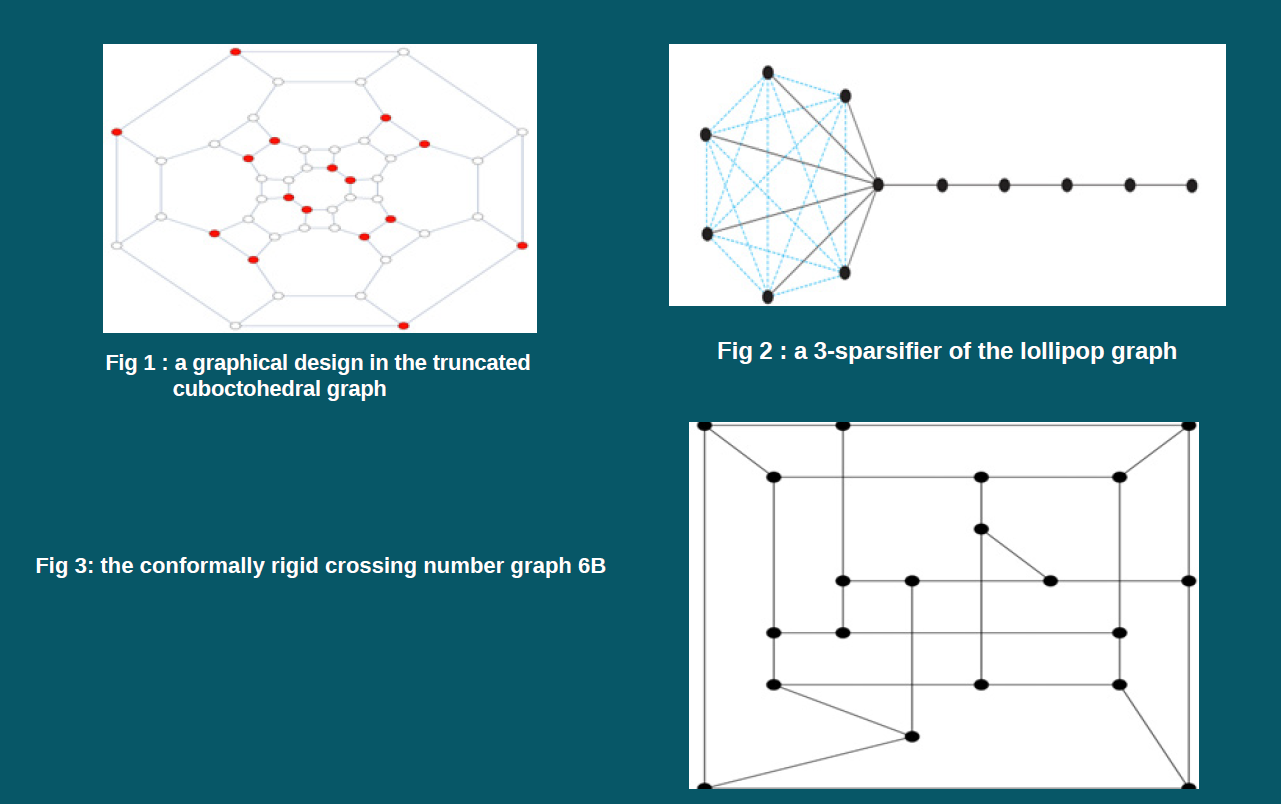
Many real-world problems are naturally modeled by graphs, with vertices representing entities and (weighted) edges representing the relationship between pairs of entities. For example, in a large data setting, one might have blood pressure information of 10,00,000 people who form vertices of a graph with edges connecting people with similar health profiles. One can compute the average blood pressure of the population by taking the weighted average of a well-chosen graphical design (a small set of people) on the graph. This will be far more accurate than a random sampling of vertices. Designs are also related to random walks and equidistribution in graphs. Graph sparsifiers are like designs in the sense that they “approximate” the original graph well in some specified sense allowing computations to scale. Graph sparsification has attracted a great deal of attention in the computer science community with the work of Spielman, Srivastava and collaborators. In this context, one can ask the question: “Which graphs cannot be sparsified nontrivially?”. This leads to a notion of conformally rigidity in graphs. This course will introduce graphical designs, graph sparsifiers and conformal rigidity in graphs. These are all concerned with the geometry of a combinatorial graph G= (V, E) and the eigenvalues and eigenvectors of its Laplacian matrix. Such problems belong, broadly interpreted, to the area of spectral graph theory; a particular novelty here are the strong ties to the geometry of polytopes, the theory of spherical designs, packing problems on graphs and coding theory. Stepping beyond combinatorics, they also connect to harmonic analysis, probability and convex optimization. Finite Cayley graphs are particularly natural, which leads to some additional influx from group theory.
Who Should Attend
• Researchers, graduate students and advanced undergraduates in mathematics, computer science and engineering.
• The only prerequisites are linear algebra and an interest in computation.
Course Fee
The participation fees for taking the course is as follows:
• Participants from abroad : US $150 (additional charges may apply)
• Industry/ Research Organizations: INR 10,000 + 18% GST
• Academic Institutions: INR 5,000 + 18% GST
• Students: INR 1,000 + 18% GST
• The above fee includes all instructional materials, computer use for tutorials and assignments, laboratory equipment usage charges, 24 hr. free internet facility. Lunch and refreshments (twice) are provided.
• The participants will be provided with accommodation on a payment basis.
Mode of Instruction
Offline (IISc Campus, Bengaluru)
Last date to apply : 25-July-2025
We now explain these problems in detail. The first problem is about graphical designs in an unweighted graph which are discrete analogs of spherical designs and Platonic bodies. It is a subset of vertices with weights so that the global average of a sufficiently smooth function on the graph agrees with the weighted average of the function on this subset. Via the powerful theory of Gale duality, designs can be organized on the faces of special polytopes. The second problem is about the geometry of graph sparsifiers (weighted subgraphs). Sparsifiers that share the initial part of the spectral information of the graph retain important global properties of the graph. The set of all such sparsifiers will be shown to be a special convex body called a spectrahedron. A combinatorial graph G= (V, E) can be thought of as a weighted graph G= (V, E, w) with the edge weights 1 for all edges. The algebraic connectivity of G is defined as the smallest non-trivial eigenvalue of the Laplacian matrix. A natural question is whether one can increase connectivity by changing the edge weights. This would, for instance, lead to faster mixing Markov chains on G. Analogously, one can look for weights that minimize the largest eigenvalue. An orthogonal take is to ask which combinatorial graphs (with edge weights 1) are already optimal for the problems of maximizing and minimizing the above eigenvalues. Such conformally rigid graphs include edge-transitive graphs, distance-regular graphs and some (but not all) Cayley graphs. Conformal rigidity can be checked via semidefinite programming (whose feasible regions are spectrahedra!), and pose several interesting open problems.
Objectives
- The key objective of this course is to expose students to several different parts of mathematics that interact with problems on graphs, namely combinatorics, convex geometry and convex optimization.
- A second goal will be to connect to applications.
- Last goal will be hands-on computation using software such as Mathematica, allowing students to experiment and discover new results.
Faculty Members

Prof. Rekha Thomas
Professor
Prof. Rekha Thomas is at the Department of Mathematics at the University of Washington in Seattle, where she is also the director of the undergraduate program. She received a Ph.D. in Operations Research from Cornell University in 1994 followed by postdoctoral positions at the Cowles Foundation for Economics at Yale University and the Konrad-Zuse-Zentrum for Informationstechnik in Berlin. Her interests are in optimization and applied algebraic geometry.

Prof. Arvind Ayyer
Professor
Prof. Arvind Ayyer is at the Department of Mathematics at the Indian Institute of Science. He obtained his Ph. D. from Rutgers University followed by postdoctoral positions at CEA Saclay and UC Davis. His interests are in algebraic and enumerative combinatorics, probability and mathematical physics.

